Publication download: Propulsion of microorganisms by a helical flagellum. B. E. Rodenborn, C.H. Chen, H. L. Swinney, B. Liu, and H. P. Zhang. Proc. Natl. Acad. Sci. USA, 110(5):E338’E347, 01 2013.
The simulation codes used to create the numerical data described below may be downloaded here. The same files are also available from the Mathworks File Exchange by searching for the “Helical Swimming Simulator.”
The swimming of a bacterium or a biomimetic nanobot driven by a rotating helical flagellum is often interpreted using the resistive force theory developed by Gray and Hancock (1955) and Lighthill (1976), but this theory has not been tested for a range of physically relevant parameters. We test resistive force theory in experiments on macroscopic swimmers in a fluid that is highly viscous so the Reynolds number is small compared to unity, just as for swimming microorganisms. The measurements are made for the range of helical wavelengths 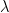 , radii
, radii 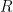 , and lengths
, and lengths  relevant to bacterial flagella. The experiments determine thrust, torque, and drag, thus providing a complete description of swimming driven by a rotating helix at low Reynolds number. Complementary numerical simulations are conducted using the resistive force theories of Gray and Hancock (1955) and Lighthill (1976), the slender body theories of Lighthill (1976) and Johnson (1980), and the regularized Stokeslet method of Cortez et al. (2005).
relevant to bacterial flagella. The experiments determine thrust, torque, and drag, thus providing a complete description of swimming driven by a rotating helix at low Reynolds number. Complementary numerical simulations are conducted using the resistive force theories of Gray and Hancock (1955) and Lighthill (1976), the slender body theories of Lighthill (1976) and Johnson (1980), and the regularized Stokeslet method of Cortez et al. (2005).
Bacterial Flagella

Movie frame showing swimming Rhodobacter Spheroides Rowland Institute at Harvard (http://www.rowland.harvard.edu/labs/bacteria).
Many microorganisms use a rotating helical flagellum for propulsion such as the Rhodobacter Spheroides shown in the image above. Because of their small size, microorganisms swim in a very low Reynolds number 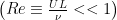 environment, where
environment, where 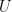 is a typical velocity,
is a typical velocity,  is a typical length scale and
is a typical length scale and  is the kinematic viscosity of the fluid. The fluid dynamics at low Reynolds number are very different from those we experience in our everyday lives. Gray and Hancock (1955) and Lighthill (1976) developed resistive force theory to describe swimming at low Reynolds number because numerical techniques to calculate the forces and torques on a swimming microorganism were not feasible at that time.
is the kinematic viscosity of the fluid. The fluid dynamics at low Reynolds number are very different from those we experience in our everyday lives. Gray and Hancock (1955) and Lighthill (1976) developed resistive force theory to describe swimming at low Reynolds number because numerical techniques to calculate the forces and torques on a swimming microorganism were not feasible at that time.
Resistive force theory continues to be used in a variety of contexts. The theory is used to interpret propulsion by a planar wave in sperm (Friedrich (2010)), small worms (Sznitman (2010)), Chlamydomonas reinhardtii (Bayly (2011)), and swimmers in a granular material (Maladen et al. (2011)); however, rather than using the drag coefficients given by Gray and Hancock or Lighthill, the coefficients are usually adjusted to fit the observations. Using drag coefficients as free parameters to fit experimental data to resistive force theory has never been proven to be a valid experimental technique. In fact, our analysis shows that whether using drag coefficients from fitting the experimental data or analytic expressions for the drag coefficients resistive force theory fails to properly describe the dynamics of a rotating helical flagellum. This failure results from a fundamental assumption in resistive force theory that long range hydrodynamic interactions can be ignored as we show below.
Flagellum Schematic
We model a bacterial flagellum as a rigid helix rotating about the helical axis. We are therefore ignoring the effects of the body of a bacterium and any flexibility in the flagellum. However, experiments have shown that a bacterial flagellum has essentially a fixed geometry when used for propulsive motion (Darnton et al. (2007)) though the flagellum may change its shape when the bacterium reverses its motor direction or due to environmental conditions.

Schematic of a helical flagellum (axis in the  direction) with radius
direction) with radius 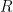 , pitch
, pitch 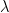 , axial length
, axial length  , filament radius
, filament radius  , contour length
, contour length 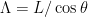 , and pitch angle
, and pitch angle  , where
, where  . The inset shows a filament segment of length
. The inset shows a filament segment of length  . The segment’s tangential unit vector is
. The segment’s tangential unit vector is ![\hat{t}(x)= \left[\cos \theta,\,-\sin \theta\sin\phi,\, \sin \theta\cos\phi\right] \hat{t}(x)= \left[\cos \theta,\,-\sin \theta\sin\phi,\, \sin \theta\cos\phi\right]](https://s0.wp.com/latex.php?latex=%5Chat%7Bt%7D%28x%29%3D+%5Cleft%5B%5Ccos+%5Ctheta%2C%5C%2C-%5Csin+%5Ctheta%5Csin%5Cphi%2C%5C%2C+%5Csin+%5Ctheta%5Ccos%5Cphi%5Cright%5D&bg=ffffff&fg=000000&s=0) , where
, where 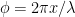 is the phase angle of the helix.
is the phase angle of the helix.
Swimming with a Flagellum at Low Reynolds Number
At low Reynolds number a rotating flagellum exerts an axial thrust 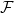 and torque
and torque  related to the flagellum’s axial velocity
related to the flagellum’s axial velocity 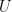 and rotation rate
and rotation rate 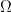 by (Happel and Brenner (1965), Kim and Karilla (1991)):
by (Happel and Brenner (1965), Kim and Karilla (1991)):
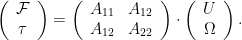
The symmetric 2 X 2 in the above matrix depends only on the geometry of the flagellum. The elements of the propulsive matrix can be determined by measuring the axial thrust 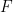 and torque
and torque  for a rotating non-translating flagellum, and the axial drag
for a rotating non-translating flagellum, and the axial drag 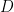 on a translating non-rotating flagellum:
on a translating non-rotating flagellum: 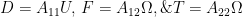 . We determine these matrix elements using experiments and numerical simulations and compare them to resistive force theory predictions for these matrix elements
. We determine these matrix elements using experiments and numerical simulations and compare them to resistive force theory predictions for these matrix elements
Resistive Force Theory
Resistive force theory obtains the total force and torque for motion of a flagellum by integrating the local forces on each small segment (see inset of Schematic above). The local forces are calculated using drag coefficients per unit length in the directions normal and tangential to the segment,  and
and  , respectively. Resistive force theory predicts that the thrust, torque, and drag on a flagellum are given by
, respectively. Resistive force theory predicts that the thrust, torque, and drag on a flagellum are given by
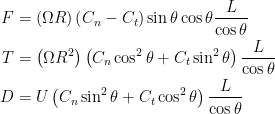
Two sets of drag coefficients are commonly used in the literature, those by Gray and Hancock (1955) and those by Lighthill (1976); both are based on slender body theory, assuming that the effect of each small filament segment is only locally important. Gray and Hancock’s drag coefficients are
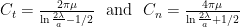
and Lighthill’s are
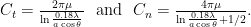
These drag coefficients are used in resistive force theory equations for the matrix elements for comparison with experiments.
Experiments

The image shows a mechanical bacterium made with a wire helix and immersed in silicone oil with viscosity 100,000 times the viscosity of water so that it is Reynolds number-matched to bacteria. 
Experiments were performed in an 80-liter tank (520 mm X 495 mm X 330 mm high) filled with silicone oil (Clearco\textsuperscript{\textregistered}) of density 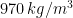 and dynamic viscosity (at
and dynamic viscosity (at 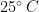 )
) 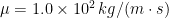 , about $100,000 times that of water. Model flagella were constructed from initially straight pieces of type 304 stainless steel welding wire with radius 0.397 mm. The wire was wrapped around aluminum mandrels with helical V-shaped grooves of varying pitches on rods with radius 6.4 mm and lengths of either 152.5 or 305 mm. Measurements were made with each flagellum’s axis about 250 mm from the tank walls to minimize boundary effects. The ends of a flagellum were kept at least 100 mm from the wall boundaries and from the free surface. To examine possible changes of the radius and wavelength of the wire helices under load, we analyzed videos for different rotation rates and for different rotation directions, and the change in wavelength and radius was smaller than the measurement uncertainty.
, about $100,000 times that of water. Model flagella were constructed from initially straight pieces of type 304 stainless steel welding wire with radius 0.397 mm. The wire was wrapped around aluminum mandrels with helical V-shaped grooves of varying pitches on rods with radius 6.4 mm and lengths of either 152.5 or 305 mm. Measurements were made with each flagellum’s axis about 250 mm from the tank walls to minimize boundary effects. The ends of a flagellum were kept at least 100 mm from the wall boundaries and from the free surface. To examine possible changes of the radius and wavelength of the wire helices under load, we analyzed videos for different rotation rates and for different rotation directions, and the change in wavelength and radius was smaller than the measurement uncertainty.
Simulations

We compute the propulsive matrix elements using a technique developed by Cortez et al. (2005), who used a “regularized” Stokeslet, which is an approximate point force, 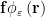 , where the radial cutoff function
, where the radial cutoff function 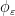 avoids singular, non-integrable kernels in numerical simulations. We also compute the propulsive matrix using the slender body theory approximation to describe flagellar swimming, as developed by Lighthill (1976) and Johnson (1980). Slender body theory uses Lorentz’s (Lorentz (1976)) result that the far field fluid response to a moving sphere can be represented by a Stokeslet and a source dipole (doublet) of the same strength at the center of the sphere. In this approach Stokeslets and doublets are arranged along the axis of the flagellum, and the force per unit length on a flagellum is obtained by inverting the integral equation relating the velocity of the flagellum’s center line and the strength of the Stokeslets and doublets. The difference between the two methods is shown graphically above.
avoids singular, non-integrable kernels in numerical simulations. We also compute the propulsive matrix using the slender body theory approximation to describe flagellar swimming, as developed by Lighthill (1976) and Johnson (1980). Slender body theory uses Lorentz’s (Lorentz (1976)) result that the far field fluid response to a moving sphere can be represented by a Stokeslet and a source dipole (doublet) of the same strength at the center of the sphere. In this approach Stokeslets and doublets are arranged along the axis of the flagellum, and the force per unit length on a flagellum is obtained by inverting the integral equation relating the velocity of the flagellum’s center line and the strength of the Stokeslets and doublets. The difference between the two methods is shown graphically above.
Comparison of Theory, Simulation, and Data

The experimental results differ qualitatively and quantitatively from the predictions of resistive force theory. The difference is especially large for  and/or
and/or  , parameter ranges common for bacteria. In contrast, the predictions of Stokeslet and slender body analyses agree with the laboratory measurements within the experimental uncertainty (a few percent) for all
, parameter ranges common for bacteria. In contrast, the predictions of Stokeslet and slender body analyses agree with the laboratory measurements within the experimental uncertainty (a few percent) for all 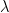 ,
, 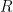 , and
, and  . Our code implementing the slender body, regularized Stokeslet, and resistive force theories will be made available on the MATLAB file exchange; thus readers can readily compute force, torque and drag for any bacterium or nanobot driven by a rotating helical flagellum.
. Our code implementing the slender body, regularized Stokeslet, and resistive force theories will be made available on the MATLAB file exchange; thus readers can readily compute force, torque and drag for any bacterium or nanobot driven by a rotating helical flagellum.
Discussion
Our experiments reveal that resistive force theory fails to provide an accurate description of low Reynolds number swimmers driven by a rotating helical flagellum for helices with  , which is the range relevant to bacteria. The measured values of thrust, torque, and drag differ significantly from the predictions of resistive force theory with either Gray and Hancock’s or Lighthill’s drag coefficients. The measurements were made for values of helical pitch
, which is the range relevant to bacteria. The measured values of thrust, torque, and drag differ significantly from the predictions of resistive force theory with either Gray and Hancock’s or Lighthill’s drag coefficients. The measurements were made for values of helical pitch 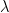 and length
and length  that include the ranges relevant to bacteria.
that include the ranges relevant to bacteria.
Hancock (1953) pioneered the analysis of swimming microorganisms more than a half century ago. His “slender body model” yielded predictions in terms of integrals that could not be numerically evaluated at that time. Then Gray and Hancock (1955) developed “resistive force theory,” which yielded expressions for thrust, torque, and drag in terms of the normal and tangential resistance coefficients.
Resistive force theory was subsequently reanalyzed by Lighthill (1976). He computed zero-thrust free swimming speed (Eq. 57 in his paper) for “an infinitely long flagellum” from his slender-body theory. He then used this computed zero-thrust swimming speed and expressions for the force distribution as “experimental data” to calibrate resistive force theory and got “improved” expressions for drag coefficients. Thus one can use Lighthill’s resistive force theory coefficients to predict the free speed for a helical flagellum without a cell body, but the theory fails when the cell body produces significant drag (non-zero thrust) (Chattopadhyay (2008)).
The primary advantage of resistive force theory has been its computational simplicity; the results are given in terms of algebraic expressions without the necessity of numerical integration. But numerical integration is now straightforward on desktop computers. We have developed numerical implementations of regularized Stokeslet theory and two versions of slender body theory, which were used to produce the curves in the figure above. These algorithms (available here) can be used by a reader to compute thrust, torque, and drag for any rotating helix with parameters 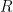 ,
, 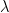 ,
,  , and
, and  .
.
In conclusion, we have shown that slender body theory and regularized Stokeslet theory predictions are in good accord with measurements on low Reynolds number swimmers driven by a rotating helix. This work indicates that it should also be straightforward to apply slender body theory to microscopic undulating swimmers, whose motion is often interpreted using resistive force theory.
1. Gray, J & Hancock, G. J. (1955) The propulsion of sea-urchin spermatozoa. J. Exp. Biol. 32, 802’814.
2. Lighthill, J. (1976) Flagellar hydrodynamics – Neumann, JV Lecture, 1975. SIAM Rev. 18, 161’230.
3. Johnson, R. E. (1980) An improved slender-body theory for stokes flow. J. Fluid Mech. 99, 411’431.
4. Cortez, R, Fauci, L, & Medovikov, A. (2005) The method of regularized Stokeslets in three dimensions: Analysis, validation, and application to helical swimming. Phys. Fluids 17, 031504.
5. Friedrich, B. M, Riedel-Kruse, I. H, Howard, J, & Julicher, F. (2010) High-precision tracking of sperm swimming fine structure provides strong test of resistive force theory. J. Exp. Biol. 213, 1226’1234.
6. Sznitman, J, Shen, X, Sznitman, R, & Arratia, P. E. (2010) Propulsive force mea- surements and flow behavior of undulatory swimmers at low Reynolds number. Phys. Fluids 22, 121901.
7. Bayly, P. V, Lewis, B. L, Ranz, E. C, Okamoto, R. J, Pless, R. B, & Dutcher, S. K. (2011) Propulsive forces on the flagellum during locomotion of Chlamydomonas Rein- hardtii. Biophys. J. 100, 2716’2725.
8. Maladen, R. D, Ding, Y, Umbanhowar, P. B, Kamor, A, & Goldman, D. I. (2011) Mechanical models of sandfish locomotion reveal principles of high performance sub- surface sand-swimming. J. R. Soc. Interface 8, 1332’1345.
9. Darnton, N. C & Berg, H. C. (2007) Force-extension measurements on bacterial flagella: Triggering polymorphic transformations. Biophys. J. 92, 2230’2236.
10. Happel, J & Brenner, H. (1965) Low Reynolds Number Hydrodynamics. (Englewood
Cliffs, NJ: Prentice Hall).
11. Kim, S & Karrila, J. (1991) Microhydrodynamics: Principles and Selected Applica-
tions. (Boston,MA: Butterworth-Heinemann).
12. Chattopadhyay, S. (2008) Ph.D. thesis (University of Pittsburgh).





